4. Calculus

4.1. Derivatives and Differentiation

Let’s develop some intuition with an example.

f(x) = 3x^2-4x

f (generic function with 1 method)

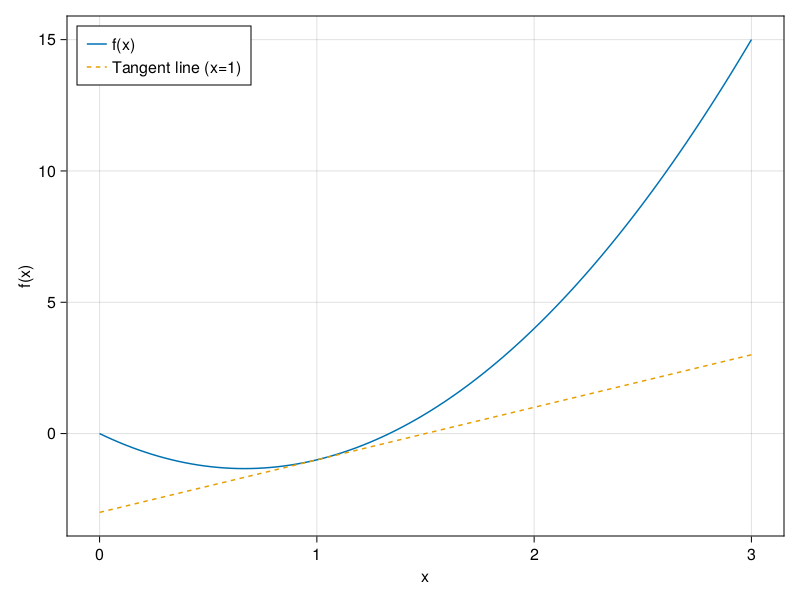
While this experiment lacks the rigor of a mathematical proof, we will soon see that indeed \( f'(1) = 2 \).

using Printf
for h in 10.0.^(-1:-1:-5)
    @printf "h=%.5f, numerical limit=%.5f \n" h (f(1+h)-f(1))/h
end

h=0.10000, numerical limit=2.30000 
h=0.01000, numerical limit=2.03000 
h=0.00100, numerical limit=2.00300 
h=0.00010, numerical limit=2.00030 
h=0.00001, numerical limit=2.00003 

4.2. Visualization Utilities

We can visualize the slopes of functions using the Makie package.

using CairoMakie

x = range(0, 3, length=100)
fg,ax = lines(x, f,label="f(x)";axis=(;xlabel = "x",ylabel = "f(x)"))
lines!(x, x->2x-3,linestyle=:dash, label="Tangent line (x=1)")
axislegend(position = :lt)
fg